Scientific Python: NumPy¶
Last update: 19. Mar 2019
NumPy: numerical computing with powerful numerical arrays objects, and routines to manipulate them. http://www.numpy.org/
[http://scipy-lectures.org/intro/intro.html#the-scientific-python-ecosystem]
NumPy is:
- vectorized
- (C) fast
- rich (not only linear algebra, but also random sampling, basic statistic, datetimes support and many more).
Prerequisites¶
- Python 3
- Python IDE
- Project folder w/ virtual environment set up
- NumPy:
$ pip install numpy
import numpy as np # NumPy import convention
Intro¶
NumPy arrays are like lists:
l = list(range(1_000_000))
print(type(l), l[:10])
a = np.array(l)
print(type(a), a[:10])
... but fast:
import time
t_start = time.time()
l_sum = sum([i*i for i in l])
print("list comprehension mul + sum took", time.time() - t_start, "seconds")
print(l_sum)
t_start = time.time()
a_sum = (a*a).sum()
print("ndarray mul + ndarray.sum took", time.time() - t_start, "seconds")
print(a_sum)
Note: NumPy methods (functions) are implemented in C. Python itself is intepreted, not compiled, hence slow. If you care for speed of your computations take care to use NumPy all along.
Note: For most of the methods/properties/operators of NumPy arrays, there exists an underlying universal NumPy function (ufunc), such as for the .sum() method above there exists np.sum() ufunc.
Exercise¶
How fast do you think sum(a*a) and np.sum(a*a) will be in comparison? Test it.
Dimensions¶
The numpy.ndarray type name stands for NumPy N-dimensional array. In Python terms these can be thought of as nested lists of numbers of equal lengths at each level of nesting.
numpy.ndarray has following size-related properties:
.ndim- number of dimensions,.shape- size of each dimension,.size- total number of elements in the array.
0D array = scalar (number), 1D array = vector (list), 2D array = matrix (list of lists), but 3D or more are also frequently used (e.g. as lists of lists of matrices rather than as tensors):
def print_dim_info(a):
print(a)
print("ndim =", a.ndim)
print("shape =", a.shape)
print("size =", a.size)
print()
num = np.array(0)
print_dim_info(num)
vec = np.array([0, 1, 2])
print_dim_info(vec)
mat = np.array([
[0, 1, 2],
[3, 4, 5],
])
print_dim_info(mat)
arr = np.array([
[
[0, 1, 2],
[3, 4, 5],
],
[
[6, 7, 8],
[9, 10, 11],
],
])
print_dim_info(arr)
Excercise¶
Without coding, can you guess output of the following commands:
vec[1],mat[:,1],arr[:,:,1]), including shape? Check your answer.What does
len()return for NumPy arrays?
Iterating over¶
for loop iterates over a first dimension of a np.ndarray array:
for i_el in vec:
print(i_el)
print()
for i_row in mat:
print(i_row)
print()
for i_mat in arr:
print(i_mat)
print()
len() value and single dim indexing correspond to the for loop behaviour, much like you would expect from nested lists:
for i in range(len(mat)):
print(mat[i])
print()
To iterate over all elements use np.nditer/np.ndenumerate
Note: NumPy arrays are stored row-wise (unlike in MATLAB where arrays are stored column-wise)
for i_el in np.nditer(arr):
print(i_el, end=", ")
print()
print()
for i, i_el in np.ndenumerate(arr):
print("a[{}] = {}".format(i, i_el))
Looking for functions¶
- Your favourite Internet search engine
- On-line reference: https://docs.scipy.org/doc/numpy/reference/
- Built-in docs:
np.lookfor('iterate over elements')
np.nd*?
Ways of creating arrays¶
You've seen already that np.array() creates NumPy array from explicit nested lists. You will usually want to create NumPy arrays in more automated fashion.
Evenly spaced vectors by step size (default: 1), like range():
np.arange(1, 11, 2)
Evenly spaced vectors by number of points (default: 50):
np.linspace(0, 1, 10)
Single value N-dim arrays:
print( np.zeros(3), "\n" )
print( np.ones(3), "\n" )
print( np.zeros((3,3)), "\n" )
print( np.ones((3,3)) * 3, "\n" )
print( np.zeros((2,3,4)), "\n" )
Diagonal matrices:
print( np.diag([1, 2, 3]), "\n" )
print( np.eye(3), "\n" ) # same as: np.identity(3)
Random samples:
# fix the random seed if needed
np.random.seed(123)
size = (2,3)
print( np.random.randint(low=0, high=3, size=size), "\n" )
print( np.random.uniform(size=size), "\n" ) # same as: np.random.rand(*size)
print( np.random.normal(size=size), "\n" ) # same as: np.random.randn(*size)
Excercise¶
- Experiment with examples above.
- Create a lower triangular 9x9 matrix:
Hint: check| 1 0 ... 0 | | 2 1 ... 0 | ... | 8 7 ... 0 | | 9 8 ... 1 |?np.eye
(*) Grid of evenly spaced "coordinates" e.g to evaluate a 2D function on a grid:
nrow, ncol = 5, 3
x = np.linspace(0, 1, nrow)
y = np.linspace(0, 1, ncol)
xx, yy = np.meshgrid(x, y, indexing="ij")
print(xx)
print(yy)
#
# for i in range(nrow):
# for j in range(ncol):
# zz[i,j] = f(xx[i,j], yy[i,j])
#
Basic data types¶
NumPy arrays elements have their data type objects numpy.dtype, corresponding to (machine-specific) C data types.
Data type of an element is accessible by .dtype property. By default, for numeric arrays, it's a float (notice the trailing .):
v1 = np.zeros(3)
print( v1 )
print( v1.dtype )
print( type(v1.dtype) )
but it can be implicitly inherited from Python objects:
v2 = np.array([0, 0, 0])
print( v2 )
print( v2.dtype )
or specified explicitly via dtype keyword argument of many array-creating functions:
v3 = np.zeros(3, dtype=int)
print(v3)
print(v3.dtype)
Data types determine a size of an array in the memory:
a10int = np.arange(10)
print( a10int.itemsize ) # in bytes; same as `a1.dtype.itemsize`
print( a10int.nbytes ) # .nbytes = .itemsize * .size
Some standard basic Python and NumPy data types and their corresponding sizes:
def print_itemsize(label, type_):
print(label, "\titemsize =", np.dtype(type_).itemsize, "bytes")
print_itemsize("Python complex", complex)
print()
print_itemsize("Python bool", bool) # bool
print()
print_itemsize("Python int", int) # long long int
print_itemsize("NumPy uint", np.uint) # unsigned long long int
print_itemsize("NumPy int16", np.int16) # short int
print()
print_itemsize("Python float", float) # double
print_itemsize("NumPy float32", np.float32) # float
print()
print_itemsize("Python str", str) # unknown size
print_itemsize("NumPy 3 char", 'S3') # max-len (byte) strings
String max-len is deduced, but note that Python3 strings are Unicode by default:
chararr = np.array(['abc', 'ef', 'g'])
print(chararr.dtype) # "<" = little-endian byte-order
print(chararr.itemsize)
Use np.chararray to create fixed size char arrays:
chararr2 = np.chararray(chararr.shape, itemsize=8)
chararr2[:] = chararr[:]
print(chararr2)
print(chararr2.dtype) # "|" = 'not applicable' byte-order
To change/cast types use .astype() method of an array:
print(chararr)
chararr3 = chararr.astype("S8")
print(chararr3)
print()
v1 = np.zeros(3)
print(v1)
v3 = v1.astype(int)
print(v3)
See arrays.dtypes reference for data types string specifiers (like S3), or structured data types (with fields) for array elements.
Indexing and slicing¶
NumPy arrays use API for indexing and slicing compatible with Python (nested) lists:
arr = np.array([
[
[0, 1, 2],
[3, 4, 5],
],
[
[6, 7, 8],
[9, 10, 11],
],
])
mat = arr[0]
print(mat, "\n")
vec = mat[0]
print(vec, "\n")
num = vec[0]
print(num, "\n")
print(vec[-1])
print(vec[:2]) # start:end (note: not including last index)
print(vec[::2]) # start:end:step
print(vec[:0:-1]) # start is deduced as len(vec)-1; end=0 is not included
NumPy throws in multi-dim indexing, either using index tuples, or directly:
print( arr )
print( arr[0, 1, 2] ) # first matrix, second row, third column; same as: arr[(0, 1, 2)]
print( arr[0, 1] ) # first matrix, second row
print( arr[0, ::-1, 2] ) # first matrix, all rows reversed (start:end deduced), third column
Views vs. copies¶
Beware: slicing doesn't copy the original array in memory, but only creates a "view" on an existing memory block. There is no implicit copy-on-write behaviour here (like in MATLAB).
vec1 = np.arange(10)
print(vec1)
vec2 = vec1[::2]
print(vec2)
vec2[:] = vec2[::-1]
print(vec2)
print(vec1) # the original array has also changed!
Use np.may_share_memory() to check if two arrays may share memory (this is a heuristic check that may give false positives).
np.may_share_memory(vec1, vec2)
You can make explicitly copies using .copy() method:
vec1 = np.arange(10)
vec2 = vec1[::2].copy() # copy, not a view
print(np.may_share_memory(vec1, vec2))
vec2[:] = vec2[::-1]
print(vec2)
print(vec1) # the original array is intact
"Fancy" indexing¶
"Fancy" indexing means indexing with boolean or integer masks, which is very convenient for filtering array elements:
vec = np.random.uniform(-1, 1, size=5)
print(vec)
mask = (vec < 0)
print(mask)
vec[vec < 0] = 0
print(vec)
vec = vec[vec != 0]
print(vec)
Using integer masks is like slicing, but with custom lists of indices for each dimension:
arr = np.diag(np.arange(1,6))
arr[:2, [0, 1]]
When using NumPy arrays for indexing, shape of the index is used in the result:
vec = 1+np.arange(10)
idx = np.array([
[1, 3],
[4, 6],
])
vec[idx]
Excercise¶
- Experiment with examples above. (What if mask has a different size? Can you combine slicing/lists and NumPy arrays in multi-dim indexing?)
- Write a
matrix_elements_atfunction that takes a matrix and list of tuples of (i,j) positons in a matrix and returns a vector of elements at these positions. Test it:matrix_elements_at(np.diag(range(4)), [(3,3),(2,2),(0,1)])should return a3, 2, 0vector.
Manipulating dimensions¶
Changes in dimensions of an array in most cases creates a view of the original array, not its copy.
Shape of an array can be changed using .reshape() method:
vec = np.arange(8)
print(vec, "\n")
mat = vec.reshape(2,4) # products of `.shape` must agree
print(mat, "\n")
arr = mat.reshape(2,2,2)
print(arr, "\n")
# .reshape() returns a view
arr[1,1,1] = 0
print(vec)
You can conveniently get a vector view (or copy) of an array of any shape using .ravel() (or .flatten()):
print(arr.ravel()) # same as: arr.reshape(np.prod(arr.shape))
print(arr.flatten()) # same as: arr.ravel().copy()
To conveniently add dimension (of size 1) to an existing array you can use numpy.newaxis in combination with slicing:
vec = np.arange(10)
print(vec)
print(vec.shape)
print()
mat_row = vec[np.newaxis,:] # single row matrix; same as: vec.reshape(1, vec.shape[0])
print(mat_row.shape)
print(mat_row)
print()
mat_col = vec[:,np.newaxis] # single column matrix (column vector)
print(mat_col.shape)
print(mat_col)
print()
In addition to .reshape() method there is also .resize() method which changes an array "in-place" and allows for size changes:
arr = np.arange(8)
print(arr, "\n")
arr.resize(2,5) # fill w/ zeros
print(arr, "\n")
arr.resize(2,2) # trim
print(arr, "\n")
Side note: np.resize() function works differently - it creates a copy and fills-up added size with repeats of the original array (not zeros):
arr2 = np.resize(arr, (3,3))
print(arr2, "\n")
print(np.may_share_memory(arr, arr2))
Transposition allows for easy re-shuffling of dimensions of an array:
mat = np.arange(6).reshape(3,2)
print(mat)
print(mat.T) # same as: mat.transpose()
where .T always reverses order of dimensions and .transpose() allows for any permutation:
arr = mat.reshape(1,2,3)
print(arr.shape)
print(arr.T.shape)
print(arr.transpose(1, 2, 0).shape)
Concatenating and splitting¶
np.concatenate([...], axis=...) concatenates arrays along given axis (default: 0); np.hstack/np.vstack are convenience functions for a first (horizontal) and second (vectical) axis:
vec = np.arange(4)
vec2h = np.hstack([vec, vec]) # same as: np.concatenate([...])
print(vec2h)
vec2v = np.vstack([vec, vec])
print(vec2v)
mat = vec.reshape(2,2)
mat2h = np.hstack([mat, mat]) # same as: np.concatenate([...])
print(mat2h)
mat2v = np.vstack([mat, mat]) # same as: np.concatenate([...], axis=1)
print(mat2v)
Opposite to concatenating functions are np.split, np.hsplit, np.vsplit, which take list of indices to split array with:
vec = np.arange(9)
# .split returns N+1 arrays, where N is nr of split indices
vec1, vec2, vec3 = np.split(vec, [3, 5])
print(vec1)
print(vec2)
print(vec3)
mat = vec.reshape(3,3)
mat_up, mat_down = np.vsplit(mat, [1])
print(mat_up)
print(mat_down)
print()
mat_left, mat_right = np.hsplit(mat, [1])
print(mat_left)
print(mat_right)
Numerical operations¶
All operations are element-wise:
vec = np.arange(5)
print( 2 * vec )
print( vec + 1 )
print( vec + vec )
print( vec * vec ) # element-wise multiplication
For dot-product and matrix multiplication use @ or .dot:
vec = np.arange(3)
print( vec @ vec ) # same as: vec.dot(vec)
print()
mat = np.ones((3,3))
mat_id = np.eye(3)
print( mat * mat_id ) # element-wise multiplication
print( mat @ mat_id ) # same as: mat.dot(mat_id)
# vector times matrix is associative
print( vec @ mat_id )
print( mat_id @ vec )
# sanity check: matrix times matrix is not associative
print( mat_id @ vec.reshape(3,1) )
print( mat_id @ vec.reshape(1,3) )
Element-wise logical operations:
a = np.array([1, 1, 0, 0], dtype=bool)
b = np.array([1, 0, 1, 0], dtype=bool)
print( np.logical_or(a, b) ) # for bool arrays same as bit-wise: a | b
print( np.logical_and(a, b) ) # for bool arrays asame as bit-wise: a & b
# but short-circuiting or/and won't work on arrays
a or b
NumPy has special numeric values np.inf, np.nan which propagate themselves as expected during vectorized numerical operations:
vec_div = np.hstack([np.ones(3), np.nan]) / np.arange(4)
print(vec_div)
print("is inf:", vec_div == np.inf)
print("is nan:", np.isnan(vec_div))
print("sum =", np.sum(vec_div))
# Note: there are built-in NaN-safe aggregations
print("nansum =", np.nansum(vec_div))
?np.nan*
All the basic math functions like np.abs, np.sqrt, np.log, np.sin etc. are implemented as vectorized functions.
Some basic array aggregations (reducing the dimension):
np.sum/np.prod: sum/product of elementsnp.min/np.max: minimum/maximum valuenp.argmin/np.argmax: index of minimum/maximum valuenp.mean/np.median: mean of elementsnp.std/np.var: standard deviation/variance of elementsnp.any/np.all: check if any/all elements areTruenp.array_equal/np.allclose: check if arrays are equal/approximately equal
Some basic array functions:
np.cumsum/np.cumprod: cumulative sum/product of elementsnp.minimum/np.maximum: element-wise minimum/maximumnp.where/np.argwhere: find elements/indices of array satysfying a conditionnp.logical_or/np.logical_and: elelemnt-wise or/andnp.sort/np.argsort: sort along an axis/using a mask
For linear see numpy.linalg module, but note that scipy.linalg module is recommended due to more efficient implementations (using BLAS and LAPACK).
If you know MATLAB, you might find this table of rough-euqivalents helpful.
Iterating to apply a function¶
If you have a pure-Python function, np.vectorize creates a convenience wrapper for a for loop
from math import sqrt
def transform(x, threshold=1):
if x < threshold:
return x*x
return sqrt(abs(x))
vec = np.random.uniform(0, 2, size=6)
print( vec )
transform_each = np.vectorize(transform)
print( transform_each(vec) )
# using kwargs
print( transform_each(vec, threshold=0) )
Use np.apply_along_axis (np.apply_over_axes) to apply function along a chosen axis (over chosen axes):
mat = vec.reshape(2,3)
# apply row-wise
print( np.apply_along_axis(transform_each, 0, mat) )
# apply col-wise
print( np.apply_along_axis(transform_each, 1, mat) )
# Note: since our transfromation is axis-agnostic, we can just apply it directly to the matrix
print( transform_each(mat) )
Remember: if possible, before using for loop / np.vectorize / np.apply_along_axis / np.apply_over_axes, check if there is a way to compute what you want using only NumPy functions.
Excercise¶
- Write a pure-NumPy implementation of
transform_eachfunction. Note: indexing creates views, not copies. - For each matrix
arr[i,:,:], wherearr = np.arrange(12).reshape(2, 2, 3), compute a sum of its all elements. Try at least two different implementations (hint:np.lookfor('sum dimension')).
Broadcasting¶
NumPy can do operations on arrays of different sizes if they can be replicated in a dimension to match a common shape.
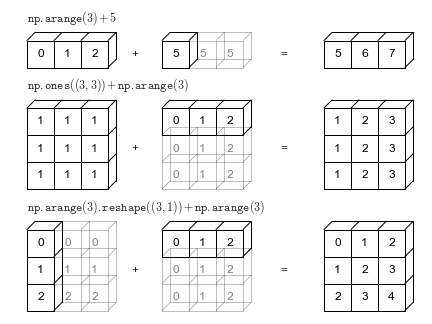Src: https://jakevdp.github.io/PythonDataScienceHandbook/02.05-computation-on-arrays-broadcasting.html
"replicated in a dimension" does not mean "cycled" - broadcasting only works with new or existing dimensions of size 1:
np.ones(8).reshape(2,4) + np.arange(2)
Excercise¶
- Add a row number to each element in a random 3x4 matrix.
- Create a 3x5 matrix of odd numbers starting with
0value at position(0,0)and increasing by2with both each row and each column:| 0 2 4 6 8 | | 2 4 6 8 10 | | 4 6 8 10 12 |